Notación vectorial unitaria | Vectores y espacios | Álgebra lineal | academia Khan
Cuando explican la Dimensión W, se representa como el lado negativo del eje X. ¿Por qué la dimensión W es X negativa? ¿No es realmente su propia dimensión?

- Intente dibujar un gráfico de 4 dimensiones en una superficie de 2 dimensiones. Esto es lo que se les ocurrió (a la derecha, aunque no es un gran gráfico).
Como ha mencionado @NendoTaka, es bastante difícil dibujar un objeto 4d en una superficie 2d.
Así es como funciona la dimensionalidad:
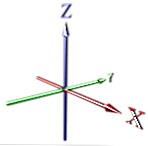
con una sola dimensión, un punto se envía infinitamente, creando una línea (Ver X)
en 2d, agregamos una dimensión perpendicular a esa (Ver X, Y).
Luego, vamos perpendicularmente nuevamente y nos expandimos hacia arriba para obtener la tercera dimensión (Ver X, Y, Z).
Debido a que 3d> 2d, no podemos representar tan bien en papel sin doblar el papel o agregar más hojas encima, todo realmente poco práctico para ver en una pantalla. Entonces, en cambio, usamos la perspectiva: cómo nuestros ojos perciben el 3D. Por lo general, los ángulos aquí son ~ 30 grados.

Y eso se ve bastante bien, porque nuestros ojos no ven en este sentido 3D tradicional, así que imitar eso funciona. Pero, cuando queremos representar una cuarta dimensión, no tenemos con qué comparar eso. Necesitamos volver a la perpendicular y esto es difícil de comprender para nuestros ojos ya que no tenemos mucha referencia.
Aquí hay una representación de ejemplo de una cuarta dimensión:
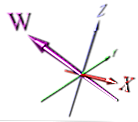
Esta es una forma más correcta de mostrar la dimensión, pero aún se basa en la perspectiva; además, no es inmediatamente obvio que sea una nueva dimensión a primera vista.
Los animadores probablemente eligieron hacer algo simple que fuera más fácil de animar. Aunque, si gira la imagen de arriba, las dimensiones X y W podrían superponerse, y esto no sería obvio en la imagen sin los punteros de flecha.
Así que sí, están equivocados, pero tampoco hay una forma sencilla de representar 4 dimensiones en una sola hoja de papel.
Coordinar fuentes de imágenes y una buena lectura
3- 1 Para ser justos, hay muchas formas estándar de proyectar objetos de 4 dimensiones como teseractos y esferas de 3 en 3 dimensiones (y luego bajar a 2 dimensiones de la manera habitual) que son muy superiores a la utilizada en el programa, muchas de los cuales tienen la ventaja adicional de verse más geniales que el utilizado en el programa.
- @senshin oh seguro, pero supongo que los animadores también querían explicar algo, en lugar de asombrar
- 1 Puede usar otras cosas además de la posición para indicar qué tan lejos de un eje está algo, como el color.